更新：ロジスティック回帰分析 | 医薬品開発のための統計解析

当サイトでは、ロジスティック回帰分析の基本的な考え方と解法を、Excel、JMP（SAS社）、R を使って理解できるように、PDF ファイルを提供しています。今回、この PDF を更新しました。

Excel を統計ソフトとして実務に使おうとするのではなく、順を追って計算過程を理解する道具として使います。最小限の数式を使いながら、より視覚的に説明しています。
Excel、JMP、R の出力結果を見比べながら、それぞれの数値の意味が理解できます。

さらに応用として、応答変数の上限が１未満のモデル、下限が 0 を越えるモデル、２本のロジスティック曲線から効力比を求めるモデルなど、いくつかのバリエーションも取り上げています。これらの事例から、最尤法によって非線形モデルをあてはめる仕組みが理解できます。
また、順序尺度の応答変数をとる累積ロジスティック回帰分析や、プロビット分析、ロバスト回帰分析などの説明もあります。

これらの PDF ファイルをダウンロードして、テキストと一緒に利用すると、効率的な学習が期待できます。
ここでは、掲載されている２つの事例（人工データ）を紹介しますので、参考にしてください。

事例１

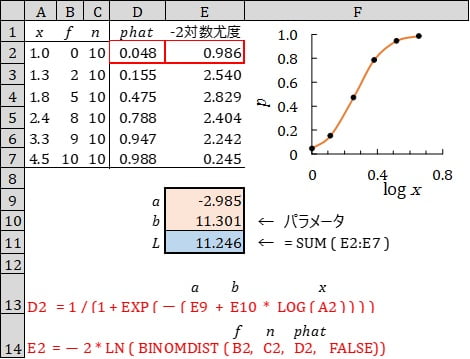
用量（\(x\)） をほぼ等比級数になるように６段階に変えて、それぞれ 10 個体（\(n\)）の動物に投与し、効果が発現した個体数（\(f\)）を計数した結果です。このデータにロジスティック曲線を最尤法であてはめます。用いるモデルは式(1)です。

$$ \hat{p} = \frac{1}{1+\exp(-(a+b \cdot \log(x)))} \hspace{10pt}(1) $$

表の右２列は、モデル式から得られた予測値（\(phat、 \hat{p} \) ）と、負の対数尤度（－２対数尤度）です。\(phat\) の列にモデル式(1)の計算式が入力してあります。例として、セル D2 とセル E2 の計算式を、13 行と 14 行に赤字で示してあります。

Excel ソルバーを使って、オレンジ色のパラメータ（\(a、b\)） を変化させ、青色のセルの負の対数尤度（\(L\)）が最小になるパラメータを求めます。この表は、ソルバーを実行した後の状態です。
負の対数尤度（\(L\)）11.246 は、カイ２乗検定の統計量になります。この 1/2 の 5.623 は JMP 出力の「損失」の値になります。

事例２

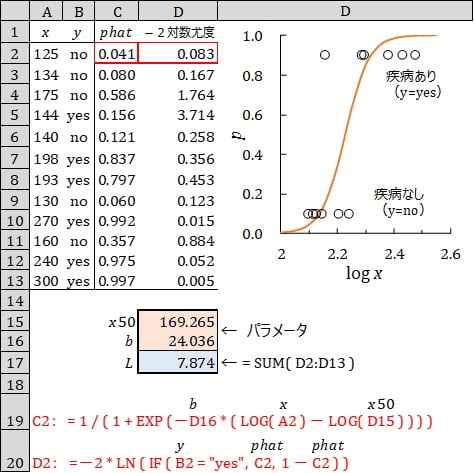
被験者 12 名のある血液成分の濃度（\(x\)）とある疾病の有無（\(y\)）の観察結果です。疾病の有無を、疾病あり（\(y=yes\)）、疾病なし（\(y=no\)）で表しています。ここにロジスティック曲線を最尤法であてはめ、疾病率が 50％ になる \(x\) の値（\( x_{50} \)）を求めます。

右のグラフには、便宜的に疾病ありの被験者（\(y=yes\)）を縦軸 0.9 に、疾病なしの被験者（\(y=no\)）を縦軸 0.1 に〇印で表しています。

ここに式(1)のモデルをあてはめることもできますが、ここでは式(2)のモデルを使います。式(2) のパラメータ \(x_{50}\) から、疾病率が 50％ になる \(x\) の値（\(x_{50}\)）を直接求めることができます。

$$ \hat{p} = \frac{1}{1+\exp(-b(\log(x) + \log(x_{50})))} \hspace{10pt}(2) $$

右２列は、モデル式から得られた予測値（\(phat\)）、負の対数尤度（－２対数尤度）です。\(phat\) の列にモデル式(2)の計算式が入力してあります。例として、セル C2 とセル D2 の計算式を、19 行と 20 行に赤字で示してあります。

Excel ソルバーを使って、オレンジ色のパラメータ（\(x_{50}、b\)） を変化させ、青色のセルの負の対数尤度（\(L\)）が最小になるパラメータを求めます。この表は、ソルバーを実行した後の状態です。
グラフのオレンジ色の曲線は、予測値（\(phat\)）と血液成分の濃度（\(\log(x)\)）との関係を表しています。
負の対数尤度（\(L\)）7.874は、カイ２乗検定の統計量になります。この 1/2 の 3.937 は JMP 出力の「損失」の値になります。

おわりに

このサイトでは、芳賀敏郎著「医薬品開発のための統計解析」（サイエンティスト社）をテキストとして、この学習を支援する PDF ファイルと R スクリプトを提供しています。
この本（グリーン本）は、第１部～第３部で構成されています。
今回、第３部第４章「ロジスティック回帰分析」の PDF ファイルを更新しました。
説明不足であった部分、舌足らずであった部分、誤記などを修正加筆してあります。

第３部「非線形モデル」
第４章　ロジスティック回帰分析
「4.1 復習」PDFファイル
「4.2 ロジスティック回帰分析（基本）」PDFファイル
「4.3 ロジスティック回帰分析（応用）」PDFファイル
（2023年1月1日）