偏相関係数の計算 | 相関・回帰

擬似相関の関係にある２変数の偏相関係数を計算することにより、第３の変数の影響を除く過程を具体的に説明します。
回帰式から予測値を得て、この予測値と観測値との差、すなわち回帰残差から偏相関係数を計算します。

事例のデータ

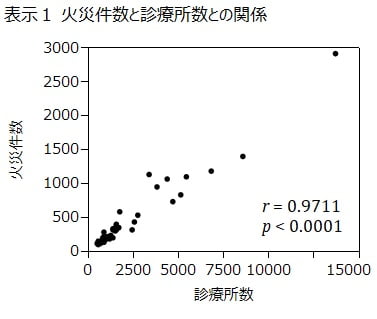
火災の発生要因をいろいろな角度から探索的に解析する中で、表示１のように、都道府県ごとに集計された2019年の建物火災出火件数（以下、火災件数）と一般診療所の数（以下、診療所数）との間に、強い正の相関があることを見出しました（$r=0.9711, p<0.0001$）。
このことから、火災の発生には診療所の数が影響しているという仮説を立てて、さらに解析を進めていくべきでしょうか。

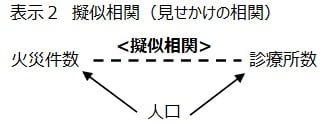
この場合は、表示２に示したように、人口が多い都道府県では火災件数が多く、人口が多い都道府県では診療所数も多いため、火災件数と診療所数との間に擬似相関（見せかけの相関）が現れたと考える方が妥当です。

そこで、表示３から、火災件数と診療所数との間で、人口の影響を除いた相関係数、すなわち偏相関係数を計算します。

なお、東京都の火災件数と診療所数は突出して多いため、表示１で見ると外れ値のようになっています。他の道府県と同じ傾向を示してはいますが、相関係数への影響が大きいことから、東京都を計算から除外しました。除外した場合の相関係数は $r=0.943$ です。

統計データは、政府統計の総合窓口（e-Stat）（https://www.e-stat.go.jp/）から取得しました。このサイトは様々なデータが得られて非常に有用です。

偏相関係数の算出

表示３のデータから、火災件数 $x_1$ を目的変数、人口 $x_3$ を説明変数とする単回帰式 (1) を得ます。同様に、診療所数 $x_2$ を目的変数、人口 $x_3$ を説明変数とする単回帰式 (2) を得ます。
\begin{eqnarray}
\hat{x}_1=38.166+0.1454x_3 \hspace{10pt} (1) \\
\hat{x}_2=81.251-0.7588x_3 \hspace{10pt} (2) \\
\end{eqnarray}

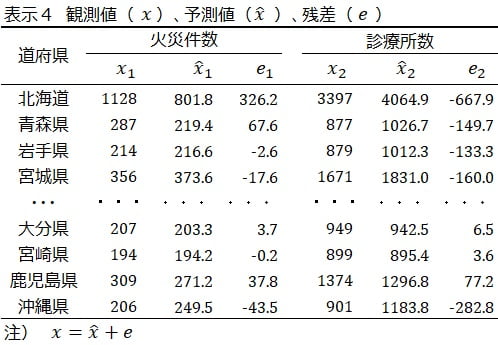
この単回帰式 (1) から式 (3) のように、道府県ごとの火災件数 $x_1$ を予測値 $\hat{x}_1$ と残差 $e_1$ に分解します。予測値 $\hat{x}_1$ は火災件数のうち人口 $x_3$ で説明できる部分、残差 $e_1$ は人口 $x_3$ で説明できない部分です。同様に、単回帰式 (2) から式 (4) のように、診療所数 $x_2$ を予測値 $\hat{x}_2$ と残差 $e_2$ に分解します。これをすべての道府県について計算して、表示４を得ます。
\begin{eqnarray}
x_1=\hat{x}_1+e_1=(38.166+0.1454x_3)+e_1 \hspace{10pt} (3) \\
x_2=\hat{x}_2+e_2=(81.251-0.7588x_3)+e_2 \hspace{10pt} (4) \\
\end{eqnarray}

たとえば、表示３および表示４の北海道を例に取ると、式 (5) および式 (6) のように分解できます。
\begin{eqnarray}
\hat{x}_1=1128=(38.166+0.1454 \times 5250)+e_1=801.8+326.2 \hspace{10pt} (5) \\
\hat{x}_2=3397=(81.251-0.7588 \times 5250)+e_2=4064.9-667.9 \hspace{10pt} (6) \\
\end{eqnarray}

表示４で、火災件数の残差 $e_1$ と診療所数の残差 $e_2$ との相関係数を計算します。これが偏相関係数で、$r_{12 \cdot 3}=-0.066$ が得られました。
見せかけの相関係数は $r_{12}=0.943$ でした。一方、人口の影響を除いた真の相関係数、すなわち偏相関係数を計算した結果、２変数の相関関係は認められませんでした。

ここまでの説明では、第３の変数として、人口 $x_3$ という１個の変数を取り上げました。仮に２個の変数 $x_3、x_4$ を取り上げるのであれば、単回帰式ではなく重回帰式を使います。たとえば、火災件数の単回帰式 (1) は重回帰式 (7) に置き換わります。
$$\hat{x}_1=b_0+b_1 x_3+b_2 x_4 \hspace{10pt} (7)$$

通常、偏相関係数 $r_{12 \cdot 3}$ は、$x_1$ と $x_2$ の相関係数 $r_{12}$、$x_1$ と $x_3$ の相関係数 $r_{13}$ 、$x_2$ と $x_3$ の相関係数 $r_{23} $ から式 (8) によって計算されます。この式は、回帰残差の相関係数の定義から導かれます（詳細は省略）。
本事例で計算すると式 (9) のように偏相関係数が得られます。回帰残差から計算した値と一致します。
\begin{eqnarray}
r_{12 \cdot3} = \frac{r_{12} – r_{13} \times r_{23}}{\sqrt((1-r_{13}^2)(1-r_{23}^2))} \hspace{10pt} (8) \\
r_{12 \cdot3} = \frac{0.94316 – 0.97813 \times 0.96778}{\sqrt((1-0.97813^2)(1-0.96778^2)} = -0.066 \hspace{10pt} (9) \\
\end{eqnarray}

母偏相関係数の無相関の検定

得られた偏相関係数から、母偏相関係数の無相関の検定を行うには、式 (10) を用いて $t$ 値を計算します。通常の２変数の相関係数の自由度は、データの組数を $n$ とすると $ (n-2)$ です。偏相関係数の自由度は、第３の変数の数を $q$ とすると $ (n-q-2) $ になります。
本事例で無相関の検定を行う必要はありませんが、試しに計算してみます。第３の変数の数は $q=1$ ですから自由度は $ (46-1-2)=43 $ です。式(11)のように $t$ 値が得られます。Excel 関数を用いて $p$ 値を求めると $=T.DIST.2T(ABS(-0.4343), 43) = 0.666$ になります。
\begin{eqnarray}
t = \frac{r_{12 \cdot 3} \times \sqrt(n-q-2)}{\sqrt(1 – r_{12 \cdot 3}^2)} \hspace{10pt} (10) \\
t= \frac{-0.0661 \times \sqrt(46-1-2)}{\sqrt(1 – (-0.0661)^2)} = -0.4343 \hspace{10pt} (11) \\
\end{eqnarray}

偏回帰係数と交絡因子

一般的に、$p$ 個の変数 $ (x_1, x_2, \cdots , x_p) $ において、２変数の組み合わせごとに相関係数を計算して、探索的に変数間の関連性を解析します。このとき、$x_1$ と $x_2 $ の相関係数を求める場合、通常の相関係数とともに、$ x_3～x_p$ の影響を除いた偏相関係数を求めます。
偏相関係数は、重回帰分析での偏回帰係数と密接な関係があります。しかし、多変量の重回帰分析よりも、２変量の相関分析における真の相関係数という意味で、偏相関係数の利用価値があります。

本事例で、偏相関係数を求めることにより、火災件数と診療所数との強い相関関係は疑似相関であることが確認できました。ここで第３の変数（背後に潜む変数）として取り上げた人口を「交絡因子」といいます。

JMP の出力結果

JMP で３変数以上の相関係数と偏相関係数を得るには、トップメニューから［分析］＞［多変量］＞［多変量の相関］と進みます。
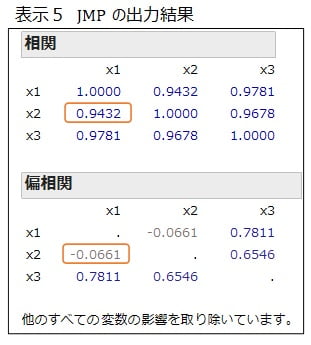
本事例を JMP で計算した結果を表示５に示します。オレンジ枠で示したように、火災件数 $x_1$ と診療所数 $x_2$ の相関係数と偏相関係数は、上記で計算した結果と一致しています。

Rの出力結果

R で３変数以上の相関係数を計算するには、 cor 関数を使います。偏相関係数を計算するには、パッケージ ppcor の pcor 関数と pcor.test 関数を使います。本事例でこれらの関数により計算した結果を表示６、表示７に示します。

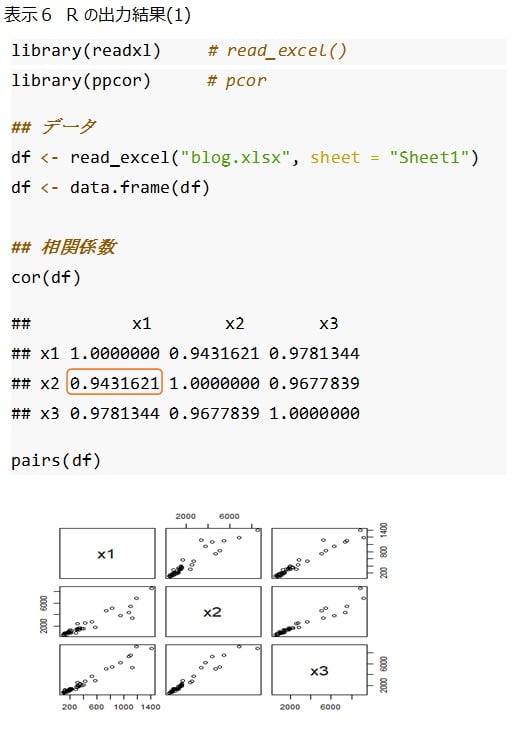
表示６で示したように、表示３の３列の変数 $x_1、x_2、x_3$ を Excel ファイル “blog.xlsx” のシート “Sheet1” から読み込み、データフレーム df に付値しました。
cor 関数は相関係数行列を出力します。オレンジ枠で示したように、火災件数 $x_1$ と診療所数 $x_2$ の相関係数は、上記で計算した結果と一致しています。
pairs 関数は散布図行列を出力します。

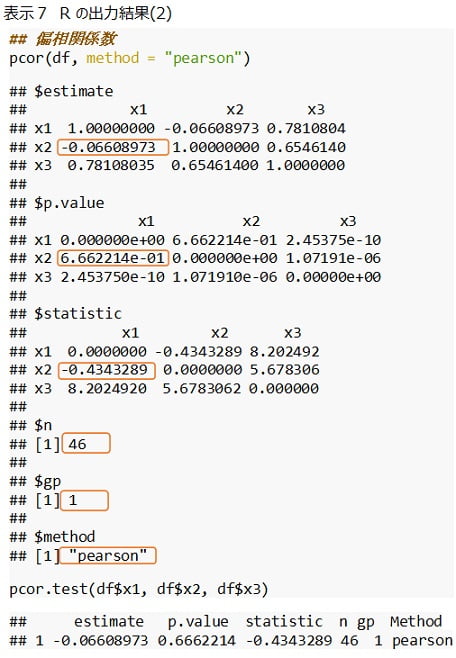
表示７で示したように、pcor 関数は偏相関係数行列を出力します。オレンジ枠で示した偏相関係数、母偏相関係数の無相関の検定の p 値（p.value）、t 値（statistic）は、上記で計算した結果と一致しています。その他、データ数（n）、第３の変数の数（gp）が表示されています。
pcor.test 関数は、２変数 $x、y$ と第３の変数 $z$ の偏相関係数を計算します。$z$ には複数の変数を指定できます。出力は pcor 関数と同じです。
なお、pcor 関数と pcor.test 関数は、引数 method に “pearson”、”kendall”、”spearman” を指定できます。デフォルトは “pearson” です。